【高校物理】熱とは？熱と温度の違い！熱容量や熱量、比熱にも分かりやすく解説

熱は頻出の分野

大学受験での頻出分野は、力学、電磁気です。大問3題なら、残り1問が波動、熱力学から出ることが多いですね。

熱力学はなんだかおおざっぱなイメージですが、実はかなり精密に作られています。

また目には直接見えない熱というものを扱うので、あなたのイメージが大事です。

そして図を書けるようにしておくことも大切です。

熱と温度の違いって何！

熱と温度なんて一緒だと思っていた人もいるかもしれません。

日常生活では、例えば、「今日は熱があるから休みます」などと使いますね。

ほぼ一緒の感覚です。

しかし物理学では熱と温度は違います。

温度とは温度計で測るもの・・・ともいえます。

熱を出した子供のおでこに手を当てて、お母さんが熱があるかどうかをみますね。

手が熱いな、と感じたら「お熱」があると言うわけです。

体温計で熱を測ると、37.5 ℃でした、と言う場合、このときの37.5 ℃が温度です。

手を当てて感じたのは、おでこから何かが手に移動したからと考えて、これを熱と呼ぶのです。

このように、高温の物体から低温の物体へ移動する「エネルギー」を熱と呼び、そのエネルギー量を熱量と呼んでいるのです。

単位はエネルギーや仕事と同じく J （ジュール）を使います。

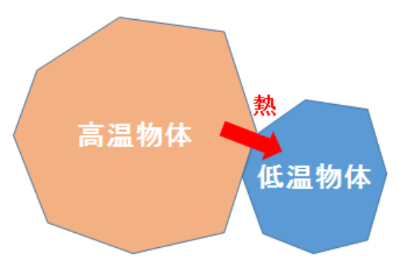
 図1

＞＞偏差値が1ヵ月で40から70に！私が実践した「たった1つのワザ」はこちら

熱平衡状態とはなんだろうか？

もう一度、図１を見てください。

高温の物体と低温の物体が接触しているとき、他に熱が移動しないとすれば、熱は高温物体から低温物体へ移動していきます。

そして図2にあるように、お互いの温度が同一になったとき、見た目には熱の移動は終わります。

これを熱平衡状態と読んでいます。

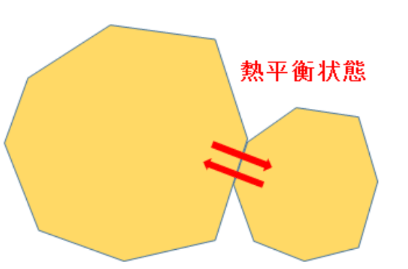
図2

難しくいわなくても、水に氷を浮かべておくと、やがて氷がとけて同じ温度になるということです。

＞＞1ヶ月で早稲田慶應・難関国公立の英語長文がスラスラ読めるようになる方法はこちら

熱容量と比熱の違いについて

熱容量と比熱の違いについていえますか？

こういう用語は、自分の言葉で他人に説明できるということが大切です。

熱容量とは・・・これは結構アバウトな感じです。

記号は大文字のCで示します。

図３にあるように、ある物体（何でもかまいません）に熱を与えると、当然温度が上がります。

このときの温度上昇分を⊿Tとしましょう。

与える熱量はQとします。

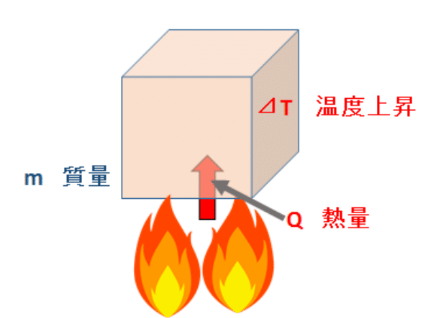
図３

ここで熱容量Cはこの物体を１ K（ケルビン）、1 ℃上げるのに必要な熱量のことです。

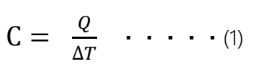
という計算式で定義されるのですね。

熱量Qを上がった温度⊿Tで割るから、１℃上げるのに必要な熱がわかるというわけです。

ここで注意してほしいのは、物体の質量には関係がないということです。

またもう少しいえば、物体が単体からできていようが、化合物であろうが、いろんな物質から混ぜ合わさってできていようが、そんなことはどうでもいいのです。

要は、この物質を１℃上げる（下げるのも同様）のにどれくらいの熱が必要かをきいているだけです。

比熱・・・・・こっちは、もう少し厳密になっています。

記号は小文字のcで示します。

記号も概念も熱容量と間違いやすいので注意してください。

比熱はその物質を1℃高めるのに必要な熱量というのは、基本的には変わりません。

ただもうひとつ条件がつきます。

「物質１g（または1 kg）について」ということ。

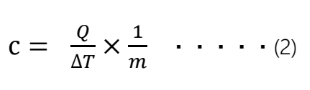
となり、さらに質量mで割っていることに注意してください。

では熱容量と比熱の違いを次の例で解説していきます。

プール1杯の水の量は、日常生活での水を扱う量から比べると莫大ですね。

このプールの水を1 ℃あげようと思ったら莫大なエネルギーが必要です。

例えば、25 mプールで、深さ1 m 幅が10 mのものを考えて見ます。
このプールをいっぱいにするために必要な水の量は、

25×10×1 = 250 m³

= 250 ton

= 250×10⁶ gです。

計算するとなんと、1 ℃上げるのに

C = 4.2×250×10⁶ × 1

= 1.05 × 10⁹ J

になります。

大きすぎてイメージしにくいですね。（計算の意味は後で解説します。）

次に家庭で水道をひねってコップ一杯の水を100g出したとします。

このときコップ一杯の水の温度を1℃上げよるための熱量、すなわち熱容量C’は420 J です。

同じ水なのにプール全体の水とコップ一杯の水ではずいぶん値が違いますね。

ここで比熱の登場です。

比熱は1 gについての値なので、当然ですが、プールの水もコップの水も1 gについては1 ℃上げるのに必要な熱量はまったく同じです。

この値は、よく知られていて4.19 J/g･K となっています。

では熱容量は使えないか・・・・というと、そういうわけでもないのです。

これは例えば実験などの時には重宝します。

容器に水を入れ、その中に熱した金属球などを入れることを考えます。

金属球の比熱を測定するという実験をします。

水の比熱はよくわかっているとします。

水のなかへ熱した金属球をなかへ放り込んで熱平衡になるのを待ち、温度が何度上昇したかを測ります。

忘れてはならないのが、容器の温度変化なのです。

金属球の持っていたエネルギーは当然、水と容器の温度上昇に使われているので、水だけを考えていては正確な実験はできません。

しかし容器は1 ℃上げるのに必要な熱量がわかってさえいれば、全体の計算は簡単に済ませることができるので、こういう場合は容器の熱容量を考えればいいのです。

前十の式 (1) (2) から変形をすることで以下の式を得ることができます。

Q= C∆T=mc∆T

よって、C=mc

これらの式は、非常に重要です。

丸暗記ということではなく、熱容量と比熱の意味を理解すれば、忘れてもすぐに出てきますね。

この意味を知るということが、難問を解く上でも非常に重要になるのです。

＞＞1ヵ月で英語の偏差値が40から70に伸びた「秘密のワザ」はこちら

熱量の保存について

図4にあるように、熱した金属球を水の中に入れることを考えます。

簡単のために、ここでは、水を入れた容器の熱容量は無視できるものとしましょう。

金属球は高温で水が低温とします。金属球を入れてしばらくすると熱平衡状態になります。

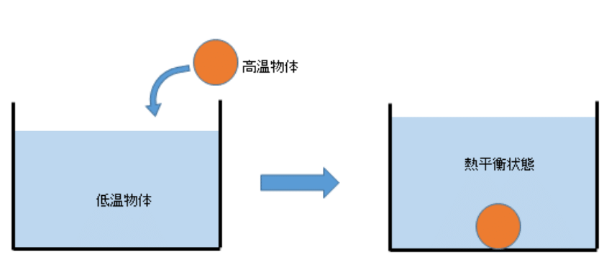
図4

このとき高温物体は熱量（熱エネルギー）を多く持っています。

水は金属球に比較すれば持つ熱量（熱エネルギー）は少ないはずです。

高温物体である金属球から低温物体の水へ熱が移動します。

そして熱平衡状態になれば、お互いの温度は同じですから熱の移動は起こりません。

熱が水と金属球の間だけでやり取りされるならば、高温物体が失った熱量は低温物体が得た熱量に等しいはずです。

これは次の例で理解してください。

兄弟がいました。

兄はお年玉を10000円もらいました。

弟はまだ小さいので2000円しかもらえませんでした。

優しい兄は、二人でお年玉を分けることにしました。

そうすると、いくらずつになりますか？

そうですね、兄、弟ともに6000円ずつで仲良く分けたのです。

ここで兄10000円（高温物体）、弟2000円（低温物体）とします。

次に、兄と弟が6000円ずつ（熱平衡状態）の状態を考えましょう。

兄の失った金額（熱量）は10000円-6000円で4000円ですね。

弟のもらった金額（熱量）は6000円-2000円で4000円となり、他に妹とかいないのであれば、これらは完全に一致することがわかりますね。

当たり前と思えるはずです。

熱の場合もこのように考えればよいのです。

もう一度書きますが、高温物体が失った熱量は低温物体が得た熱量に等しい。

ここをよく理解してください。

他に熱（お年玉）をもらう容器（妹？）がある場合も、この考えに従って同様に考えればいいのです。

物理学で大事なことは、なぜ？です。

そして用語理解と定義がとても重要です。

これらをおろそかにして、問題集を何度もやっても応用力がつきません。

基本理解を心がけてください。