
「数学Ⅲの勉強法」
のページにおいて私は、多くの単元において、“数学の学習の大部分は、解法習得と訓練による習熟である”事を繰り返し申し上げてきました。
(※これはあくまで大学入試レベルにおいての話です。数学の研究を行うレベルになると、当然ながら才能・発想力が必要となります。)
実は、その「解法習得と訓練」の際に、1つ注意点があるのです。
確かに各々の公式・各々の解法に熟達する事は必要なのですが、 “各々の公式や解法の根底に共通する考え方は何だろうか”という事に意識を向けてほしいのです。
例えば、数学Ⅰで最初に学習する「数と式」の単元では
「比例式の問題 → =k とおく」
「対称式ではx+yとxyで表す」
「x^2=Xと置き換える」
といった、様々な解法テクニックが登場してきます。
これらを、特に何も考える事なく解法を覚えていっても、問題は一応解けるようにはなるのですが、これが応用問題になると「どの解法を用いればよいのか」が一見すると分からない問題も多く、結果、ペンが止まってしまうという事態に陥ります。
その為、基本問題を解く段階で、
“これら個々の解法テクニックは、何を目的としているのか”
“なぜ解法テクニックとして教えられているのか”
と、考察して頂きたいのです。
「比例式の問題 → =k とおく」
「対称式ではx+yとxyで表す」
「x^2=Xと置き換える」
こういった個々の解法に共通する「目的」は何だと思いますか?
頭の良い皆さんであればもうお分かりでしょう。
そうです、“式をなるべくシンプルにして、計算しやすくし、値を求めやすくする事”ですね。
「比例式の問題 → =k とおく」理由は、文字を減らして式をシンプルにする為です。
「対称式ではx+yとxyで表す」理由は、式変形によって数式の様々な項を全てx+yとxyで表せる形にする事で、そこに数値を代入出来る形にして、最終的に式をシンプルにする為です。
「x^2=Xと置き換える」理由は、二乗の項を一乗の文字に置き換える事で、式をシンプルにする事で因数分解をしやすくする為です。
>>1ヶ月で早稲田慶應・難関国公立の英語長文がスラスラ読めるようになる方法はこちら
字面上の形は違えど、全て目的は同じでしょう?
「これらは全て、『文字をなるべく減らす為』『次数をなるべく減らす為』のテクニックなのだ」
「文字や次数を減らす事でスッキリさせて計算しやすくする為に、様々な解法は存在するのだ」
こういう“問題の背景”が分かっていると、“個別の解法が、全て同一の主旨に基づいているもの”だという事が体系的に分かってくるのです。
上記の例だけではなく、“表面上の解法は違っていても、事実上の目的は同一である”解法は数多く存在します。
そのようにして、種々の基本問題の解法テクニックを体系的に理解していると、各単元における見通しがよくなり、かなり頭に入りやすくなります。
効果はそれだけではありません。
先程の例で申しますと、個々の解法の目的は“式をなるべくシンプルにして、計算しやすくし、値を求めやすくする事”でしたね。
それでは、「数と式」に関する、初見の応用問題に出会った際にはどうすればよいと思いますか?
そうです、“この逆の考え方を利用すればいい”のです。
例えば、「数と式」のある応用問題が出題されたとします。
その問題は一見複雑な数式で、字面上、今までの基本問題の形、「=k とおく」タイプとも「基本対称式で表す」タイプとも「x^2=Xと置き換える」タイプとも違う、まさに初見の問題です。
この時、前述しました“問題の背景”を知らない人ならば、「何だこれ…全然見た事ないタイプの問題だ。解き方分からない……。」となり、止まってしまいます。
>>1ヵ月で英語の偏差値が40から70に伸びた「秘密のワザ」はこちら
一方、“問題の背景”を知っている人ならば、
「これは複雑な数式だから……まずは式をシンプルにして、計算しやすくする事を目的に考えていこう。式をシンプルにする方法は……『代入する』とか『文字を消去する』とか『文字を置き換える』とか『基本対称式で表す』とかが、手法としてあったぞ。色々と試してみるか……」と、問題の指針を自分で立てる事が出来るようになるのです。
つまり、“個々の解法パターンの知識習得 → それらに共通する背景を知る”の逆、
“背景を知っている → 初見の応用問題に対し、同じ背景下にある数種の解法パターンを使用してみる”
という手段を用いて応用問題に挑戦していくのです。
そして、これこそがまさに、
“応用がきく”
“自力で(暗記せずに)問題が解けるようになる”
という事、巷で言われる『数学力』の正体なのです。
「個別の解法パターンの背景を知る」事が、初見の応用問題を解けるようになる為の秘訣なのです。
個別の解法の「背景」を知っておく事がいかに重要であるかが、少しでもお分かり頂けたでしょうか?
数学の学習において、常にこうした見通しをきちんと持っておく事は非常に大切なのですが、残念ながら、多くの参考書では、各問題ごと・各解法ごとの解答の詳しい解説はされていても、こうした「背景」についての説明をされていないのです。
ですから、数学の学習者であるあなた達1人1人が、基本問題で解法を習得する際にも、自ら意識して、
“これらの解法に共通する、背景(目的・意図)は何だろう?”
“この背景を知っていれば、どのような問題において自力で考えられるだろう?”
と問いながら、数学の学習を進めていってほしいのです。
⇒1ヵ月で英語の偏差値が40から70に伸びた「秘密のワザ」はこちら
⇒【1カ月で】早慶・国公立の英語長文がスラスラ読める勉強法はこちら
⇒【速読】英語長文を読むスピードを速く、試験時間を5分余らせる方法はこちら
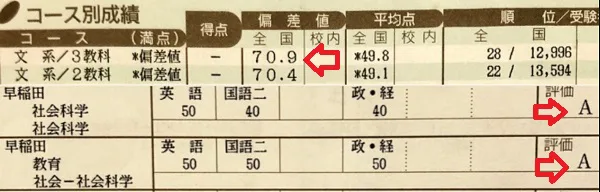
現役の時に偏差値40ほど、日東駒専に全落ちした私。
しかし浪人して1ヶ月で「英語長文」を徹底的に攻略して、英語の偏差値が70を越え、早稲田大学に合格できました!
私の英語長文の読み方をぜひ「マネ」してみてください!
・1ヶ月で一気に英語の偏差値を伸ばしてみたい
・英語長文をスラスラ読めるようになりたい
・無料で勉強法を教わりたい
こんな思いがある人は、下のラインアカウントを追加してください!
筆者は現役時代、偏差値40ほどで日東駒専を含む12回の受験、全てに不合格。
原因は「英語長文が全く読めなかったこと」で、英語の大部分を失点してしまったから。
浪人をして英語長文の読み方を研究すると、1ヶ月で偏差値は70を超え、最終的に早稲田大学に合格。
「1ヶ月で英語長文がスラスラ読める方法」を指導中。
⇒【秘密のワザ】1ヵ月で英語の偏差値が40から70に伸びた方法はこちら
⇒【1カ月で】早慶・国公立の英語長文がスラスラ読める勉強法はこちら
⇒【速読】英語長文を読むスピードを速く、試験時間を5分余らせる方法はこちら











