【高校物理】振り子の勉強法を解説！公式を使った問題の解き方のコツ！

物理で出題される振り子とは、多くは「軽くて伸びない糸の下端に質量mの質点とみなせる物体をつなげたもの」。

あるいは糸の代わりに、軽いバネを使うこともよくあります。

その振らせ方には大きく二通りの方法があります。

・鉛直面内で振らせる。

・水平面内で円を描くように回転させる。円錐振り子

問題として出てくるのはこのどちらかがほとんどですが、振り子を振らせる場所についてはいろいろ考えられます。

地球重力下で、月面で、エレベーターや電車などの加速する乗り物の中でなど。

その他、問題のバリエーションとしては、糸が途中で釘に引っかかったり、糸が切れて物体が飛んでいくというようなものがあります。

＞＞1ヶ月で早稲田慶應・難関国公立の英語長文がスラスラ読めるようになる方法はこちら

鉛直面内で振らせる場合

まず一番単純な「鉛直面内で振り子を振らせる場合」について考えていきます。

これは振り子を振らせているイメージです。

まずは振り子を図１のように鉛直に対して直角に持ち上げて静かに離すことを考えます。

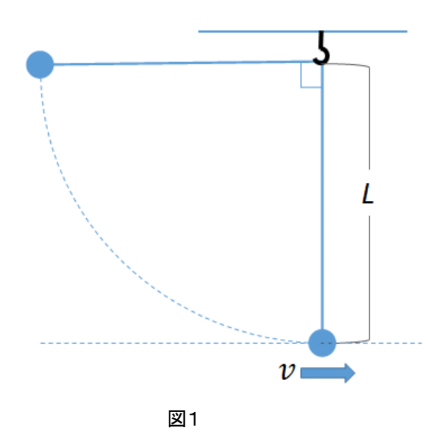
最初に下端での振り子の速さを求めていきましょう。

この場合、振り子は直線運動をしないので運動方程式を立てて解くのは難しくなります。

ではどうするかというと、エネルギーを使うと簡単に解くことができます。

ここでは、空気抵抗などがないと仮定して話を進めます。

振り子の長さを L 、重力加速度を g 、最下端でのおもりの速さを ｖとしましょう。

おもりの質量は m としておきます。

力学的エネルギー保存の法則を考えます。

位置エネルギーの基準を最下点での水平面にとります。

したがって、最初の位置での位置エネルギーは　mgL、 運動エネルギーは0となります。

最下点における位置エネルギーは0運動エネルギーは1/2 mv²。

力学的エネルギー（位置エネルギー＋運動エネルギー）が保存されるので、

mgL+ 0 = 0 + 1/2 mv²が成立します。

よって、この式からv=√2gLとなります。

当然ですが、抵抗等がない場合、振り子のおもりの質量 m は速さには無関係です。

＞＞1ヵ月で英語の偏差値が40から70に伸びた「秘密のワザ」はこちら

振り子を途中から振らせると・・・

次はもう少し難易度を上げてみましょう。

図２にあるように振り子を鉛直から角度θの位置から静かに離します。

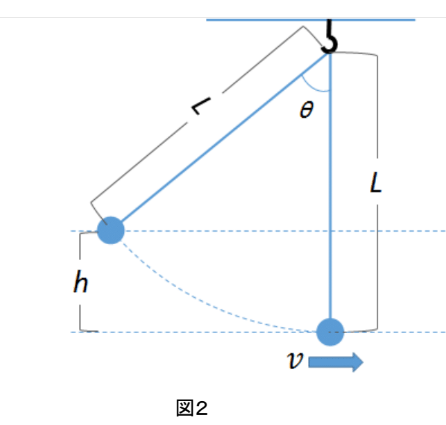
このときの最下点での物体の速さvを求めます。

同じようにエネルギーを使えば簡単に解くことができます。

最下点を含む水平面を位置エネルギーの基準面とします。

最下点から最初の物体の位置までの高さをh としてエネルギー保存を考えましょう。

最初の位置での位置エネルギーはmgh運動エネルギーは0。

最下点における位置エネルギーは0運動エネルギーは　1/2 mv²。

力学的エネルギー（位置エネルギー＋運動エネルギー）が保存されるので、

mgh+0=0+1/2 mv²が成立します。

よって、この式からv=√2ghとなります。

ここで h をL とθ をつかって表すことを考えます。

図３を見てください。

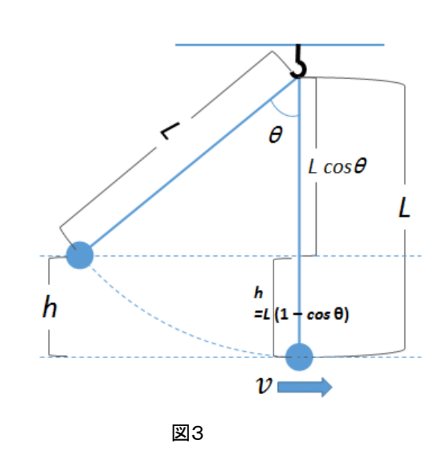
糸の長さはどこでも変わらずLです。また最下点からの高さhのところから糸の上端の結び目までの長さは、三角関数を使うことでL cosθとなることがわかります。

よって、

h=L−L cosθ

h=L(1−cosθ)

となります。

したがってv=√2gL(1−cosθ)。

さらに難易度を上げていきましょう

では、図４のような場合はどうなるでしょうか。

角度θのところから物体を静かに離して、角度φの位置に来たときの速さv′を求めましょう。

ただし　θ>φ ,　0 <θ <π/2とします。

最下点よりhの高さから物体を静かに離して、h'の高さにきたとします。

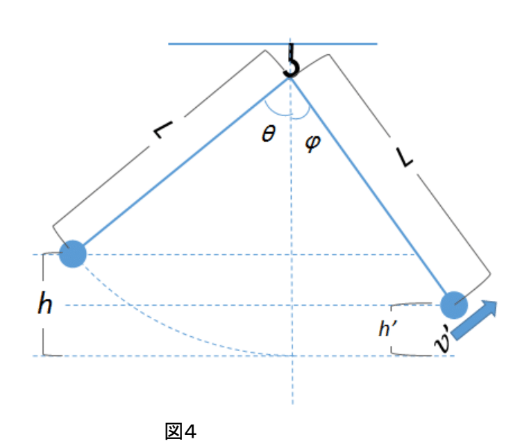
最初の位置での位置エネルギーはmgh、運動エネルギーは0。

h' の高さの地点における位置エネルギーはmgh'    運動エネルギーは1/2mv′²。

力学的エネルギー（位置エネルギー＋運動エネルギー）が保存されるので、

mgh+ 0 = mgh'+1/2mv′²が成立します。

よって、この式から

v′=√2gL(h−h')となります。

先ほどと同様に

h=L(1−cosθ)

h'=L(1−cosφ)

を代入すると答えが得られます。

v′=√2gL(cosφ−cosθ)

もし糸が切れたら・・・？

先ほどの図４において角度φ の位置に来たときに、突然糸が切れたとします。

さて、その後の物体は次の ア ～ ウ のどの軌道を飛ぶでしょうか？

理由も考えてください。エネルギーで考えて見ましょう。

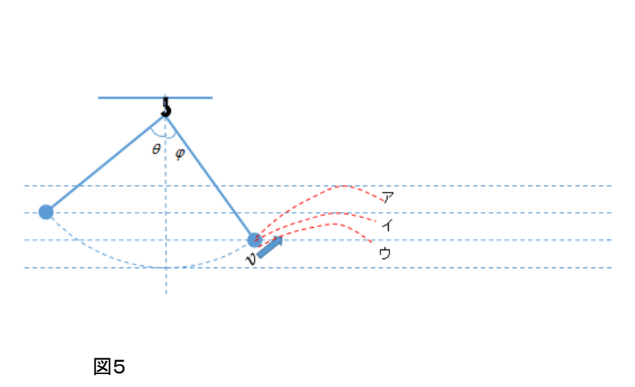
答えはウ。

エネルギーが保存されるということから、イだと考えてしまいがちです。

しかし図5にあるように、物体の飛び出すときの速度は鉛直方向に対して斜めなので、そのときお物体の速度は水平方向と鉛直方向に分けて考えられます。

このとき水平方向には力が働かない（鉛直方向には重力が働く）ので物体は水平方向には仕事を受けず、水平方向の速度は変化しません。

ということは、放物運動の最高点において、物体の鉛直方向の速度は 0 になっても水平方向の速度（ここでは [数式]とします）は0にはなりません (図６)。

放物軌道での最高点での物体の運動エネルギーは 0 とならないのです。

飛び出した後の最高点の基準面からの高さを h '' として力学的エネルギー保存の式を立ててやると、

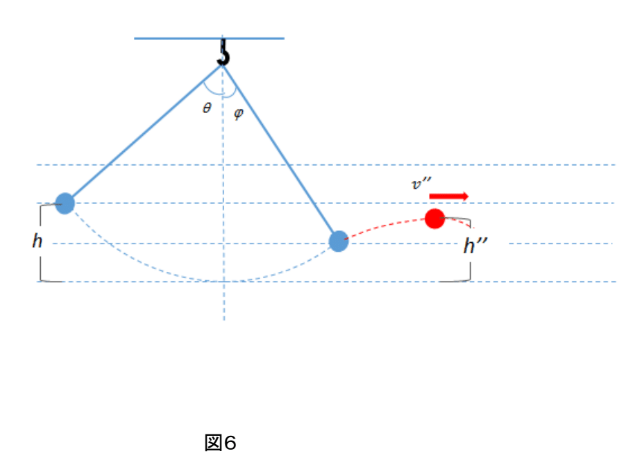
最初の位置での位置エネルギーはmgh、運動エネルギーは0。

h ''の高さの地点における位置エネルギーはmgh''、運動ネルギーは1/2mv′'²。

力学的エネルギー（位置エネルギー＋運動エネルギー）が保存されるので、

mgh+ 0 = mgh'' + 1/2mv′'²

これを変形して

h'' =h − v′'²/2g < h

となり、 h’ はhより小さくなります。

高校物理の振り子の問題の解き方まとめ

力学は物理学の基礎であり、他の分野の理解にもとても大切です。

ここではエネルギーを考えて振り子問題を考えました。

その他、振り子の問題にはいろいろなバリエーションがあります。

振り子の単振動や等時性、円錐振り子、加速する車内での振りこの運動などについても勉強していきましょう。