
大学受験における1次関数の概要
大学受験の数学において重要な単元の一つが、1次関数。
二次関数を解く際にも、1次関数を利用することもあります。
1次関数の概要としては2つの変数x、yがあるとき、1次関数は次の式で表されます。
y=ax+b(ただし、a,bは定数とします)
重要な定義なので、必ず覚えといてください。
またy=f(x)とも表します。
a=0のときy=bとなるので、xがどんな値になってもy=bとなります。
これを定数関数と呼びます。
また関数y=f(x)について、x=pのときのyの値をf(p)で表し、x=pの時のf(x)の値がf(p)となります。
例としてはf(x)=3x-4のとき、f(3)=3×3-4=5となり、この5という数字が値となります。
関数y=f(x)について、xのとりうる値の範囲をこの関数の定義域と呼びます。
xが定義域の中のすべての値をとるときのyの値を値域と呼びます。
定義域が設定されていないときはすべての実数で考えることが多いです。
例 y=3x-4(xの範囲記述なし)定義域→すべての実数
値域→すべての実数
y=3x-4(1≦x≦4)定義域→1≦x≦4
値域→‐1≦x≦8
関数のグラフとしては、y=f(x)のとき、座標平面上での(p,f(p))を座標にもつ店全体からなる図形をy=f(x)のグラフと表現します。
これは2次関数でも使います。
グラフとしては、y=ax+bのa、bの部分、つまりは傾きによって変わってきます。
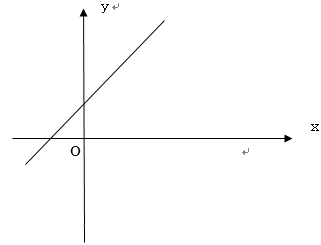
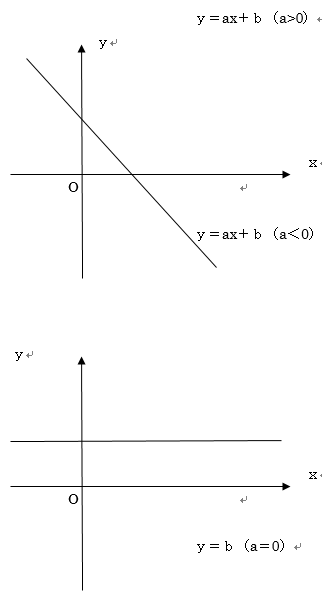
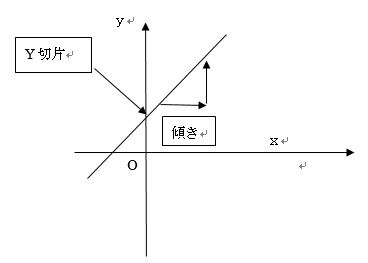
このようにaがかわることにより正か負かで変わってきます。
関数y=f(x)においてその値域に最も大きな値があるとき、その値を最大値、最も小さい値を最小値といいます。
xの定義域の端と端、例えば‐1≦x≦1のx=‐1と1のとき、yは最大値、最小値となることが多いです。
またa>0の時はxの数字が小さいほうが最小値、大きいほうが最大値を取ります。
ここではx=-1のほうが小さいので最小値、x=1の時が最大値になります。
a<0のときは逆で数字が小さいほうつまりはx=-1の時が最大、大きいほうが最小値を取ります。
a>0 xの定義域の小さいほう→yは最小値 大きいほう→yは最大値
a<0 xの定義域の大きいほう→yは最小値 小さいほう→yは最大値
大学受験における1次関数の勉強法
xの定義域、yの値域の指定をして、傾きとy切片を求める問題が頻出。
例えば、a>0のとき、y=ax+b(-1≦x≦1)で、(0≦y≦2)のときaとbの値を求めよというような問題。
このときはxの範囲の端と端が最大、最小となるので(x、y)=(-1,0),(1,2)を代入し0=-a+b,2=a+bという二次方程式になり、これをとくと、a=1,b=1となります。
xyの定義域、値域を書かずにf(x)=ax+bとする、f(-1)=0,とf(1)=2のときのa,bを求めてくださいという問題も良く見られます。
さっきの問題と全く同じことを聞いており、同じ、a=1,b=1となります。
このように形を変えて出題されるので、たくさん演習して慣れておかなければいけません。
またグラフを書かせる問題も出ますので、自分でグラフを書く習慣もつけておきましょう。
⇒1ヵ月で英語の偏差値が40から70に伸びた「秘密のワザ」はこちら
⇒【1カ月で】早慶・国公立の英語長文がスラスラ読める勉強法はこちら
⇒【速読】英語長文を読むスピードを速く、試験時間を5分余らせる方法はこちら
現役の時に偏差値40ほど、日東駒専に全落ちした私。
しかし浪人して1ヶ月で「英語長文」を徹底的に攻略して、英語の偏差値が70を越え、早稲田大学に合格できました!
私の英語長文の読み方をぜひ「マネ」してみてください!
・1ヶ月で一気に英語の偏差値を伸ばしてみたい
・英語長文をスラスラ読めるようになりたい
・無料で勉強法を教わりたい
こんな思いがある人は、下のラインアカウントを追加してください!
筆者は現役時代、偏差値40ほどで日東駒専を含む12回の受験、全てに不合格。
原因は「英語長文が全く読めなかったこと」で、英語の大部分を失点してしまったから。
浪人をして英語長文の読み方を研究すると、1ヶ月で偏差値は70を超え、最終的に早稲田大学に合格。
「1ヶ月で英語長文がスラスラ読める方法」を指導中。
⇒【秘密のワザ】1ヵ月で英語の偏差値が40から70に伸びた方法はこちら
⇒【1カ月で】早慶・国公立の英語長文がスラスラ読める勉強法はこちら
⇒【速読】英語長文を読むスピードを速く、試験時間を5分余らせる方法はこちら











