
数学Ⅱおよび数学Bの勉強法を単元別にお伝えしていきます。
数学Ⅱおよび数学Bの単元も、2015年度入試より新課程となり下記の様に変更になっています。旧課程の方々はご注意下さい。
数学Ⅱ
1.いろいろな式 (旧課程の「式と証明・高次方程式」に相当します。)
2.図形と方程式
3.指数関数・対数関数 (旧課程の「いろいろな関数」の一部に相当します。)
4.三角関数 (旧課程の「いろいろな関数」の一部に相当します。)
5.微分・積分の考え
数学B
1.確率分布と統計的な推測 (旧課程・数学Cの「確率分布」「統計処理」がこちらで扱われます。)
2.数列
3.ベクトル
数学Ⅱ(旧課程)
1.式と証明・高次方程式
2.図形と方程式
3.いろいろな関数
4.微分・積分の考え
数学B(旧課程)
1.数列
2.ベクトル
(3.統計とコンピュータ (旧課程においても選択単元。新課程では廃止されました。)
(4.数値計算とコンピュータ (旧課程においても選択単元。新課程では廃止されました。)
数学Ⅱ・数学Bにおいては、一部移行や廃止があるものの、さしたる変化はありません。
>>1ヵ月で英語の偏差値が40から70に伸びた「秘密のワザ」はこちら
数学Ⅱ・数学Bの単元別勉強法
いろいろな式
基本的な計算テクニックは、数学Ⅰの「数と式」で既に学んでいるわけですが、この単元では、扱う対象である「数」「式」の範囲を更に拡張させていきます。
「等式・不等式の証明法」「剰余」「高次方程式」「相加・相乗平均」「複素数」など、新たな内容は盛り沢山ですが、既にかなりの解法を「数と式」の単元で習得済の方々であれば新たに習得しなければならない解法はそれ程多くありません。
勉強方法は「数と式」の単元で実行した方法と基本的に同じく「解法習得&訓練」です。
>>1ヶ月で早稲田慶應・難関国公立の英語長文がスラスラ読めるようになる方法はこちら
図形と方程式
この「図形と方程式」では、今まで図形問題を解く際に、補助線を引いたり、長さや角度を求めたり、あくまで「図形的にしか」扱えなかった図形を“数式で置き換え表現”して扱う事が出来るようになる単元です。
大学以降の数学では「代数幾何学」と言いますが、この「図形と方程式」という単元では、その代数幾何学の基本を学びます。
なぜ数式的(代数的)に表現する方が良いのか。
それは“(数式を、計算したり、変形したり、文字や式を代入したりetc) 数式の状態ならば、図形を図形のまま扱うよりも、格段にいろいろな操作がしやすく、図形のもつ性質を精密かつ簡明に調べられるから”です。
この単元を学習する際は、常に頭の中に
数式⇔図形
の「相互変換意識」を持ちながら、学習を進めていって下さい。
例えば、
「y=ax+b ⇔ 直線」
「(x-a)^2 + (y-b)^2 = r^2 ⇔ 円」
といった意識です。
この意識をもっているか否かで、途中計算において数式を変形したとしても、「その数式は図形的に何を表しているのか」という「数式の本質」を見失わずに済みます。
演習方法は基本的に他単元と同様、解法の習得&訓練です。
>>1ヵ月で英語の偏差値が40から70に伸びた「秘密のワザ」はこちら
指数関数・対数関数
指数・対数がなぜ発見(発明)されたのか。
それは、“もの凄く大きな桁数の数、あるいは、もの凄く小さな桁数の数(小数点以下何桁もあるような小さい数)を扱う際に、その扱いが非常に容易になるから”です。
卑近な例を出しますと、「10000000000000」と表記しなければならなかった数を、指数を用いれば「10^13」と簡潔に表現出来るようになります。
また、指数部分の「13」という数字に着目したい時は、対数を用いて「13= log10 10000000000000」と表記を換えれば、「10が何乗されているか (10000000000000の、先頭の1の後に何桁0がついているか)」がパっと一目で分かるようになります。これが、指数・対数の便利さです。
この単元の学習も、基本的には解法パターンを習得&訓練なのですが、上述した「便利な道具に習熟する為」という意識を頭の片隅に入れておきながら学んでいって下さい。
学習目的が分かっていれば、大学以降でも、指数・対数がどのような状況で使用されているのかが明確に分かるようになります。
>>偏差値が1ヵ月で40から70に!私が実践した「たった1つのワザ」はこちら
三角関数
基本的には数学Ⅰ「図形と計量」で述べた事と同じ方法です。
解法を1つ1つ習得し、コツコツと訓練をして下さい。
微分・積分の考え
微分・積分は、高校数学のメインと言っても過言ではありませんし、大学でも理系の学問を中心に、様々な分野で利用されています。
学習方法ですが、まずは、微分・積分の基本的計算に慣れ、四則演算と同じ感覚で出来るようにしましょう。
同時に、極限の概念をしっかり理解しておきましょう。
(※極限について。厳密には、大学数学でε‐δ論法というのを習うまで高校数学の段階では曖昧な説明がなされているのですが、とりあえず「そういうものだ」と思っておいて頂ければそれでも構いません。)
そして、またまた解法の習得と訓練です。微分・積分は覚えるべき解法が多いので大変ですが、根気よく勉強していって下さい。
数学Ⅲの「微分法」「積分法」も学習する理系の方々は、ここで学習する内容がその基礎となります。(数学Ⅲでは扱う関数が変わるだけです。)
また、微分の応用問題の出題パターンは数学Ⅰ「二次関数」のパターンとよく似ています。
二次関数が苦手な人はそちらの克服を急いで下さい。
>>偏差値が1ヵ月で40から70に!私が実践した「たった1つのワザ」はこちら
確率分布と統計的な推測
基本的には数学A「場合の数と確率」で述べた事と同じ方法です。
“問題文で問われている内容を正確に読み取れているか”
“読み取った内容を適切な数式・記号で表現出来ているか”
をチェックしながら、演習を重ねていって下さい。
数列
数列分野では、「等差数列」「等比数列」「階差数列」「群数列」「漸化式」「数学的帰納法」全てにおいて、解法パターン・主題パターンが決まっています。
そのため、とにかく各解法パターンに習熟すれば、大抵の問題は解けるようになります。
演習を重ねるほど「似たような問題ばっかり」だという事が分かってきます。
加えて、漸化式は確率と絡めて、また、数学的帰納法は整数問題と絡めて出題される事が多いですので、そういった融合問題にも習熟しておきましょう。(融合問題の解法もパターンが決まっています。)
>>偏差値が1ヵ月で40から70に!私が実践した「たった1つのワザ」はこちら
ベクトル
指数・対数と同様、ベクトルも「便利な道具」なのです。
ベクトルには(スカラーと違い)「大きさ」だけでなく「向き」もあります。
(※厳密には、ベクトルの定義は「大きさと向きをもったもの」とは少々異なるのですが、高校数学の範囲ではその定義で充分ですので、深くは触れない事にします。)
この考えを用いれば、“1次元(数直線)・2次元(座標平面)・3次元(座標空間)と、それまで別々に扱っていたものが、「ベクトル」という概念によって、異なる次元を通じて統一的に扱う事が可能になる”のです。
これが、ベクトルの便利さ・最大の利点です。
勉強法ですが、まずは各概念を、その概念が作られた理由も含めてしっかり理解して下さい。
「なぜ『内積」という概念があるのだろう」
「なぜ『位置ベクトル』という概念があるのだろう」
といったように、です。
あとは問題演習で、解法の習得&訓練です。
⇒1ヵ月で英語の偏差値が40から70に伸びた「秘密のワザ」はこちら
⇒【1カ月で】早慶・国公立の英語長文がスラスラ読める勉強法はこちら
⇒【速読】英語長文を読むスピードを速く、試験時間を5分余らせる方法はこちら
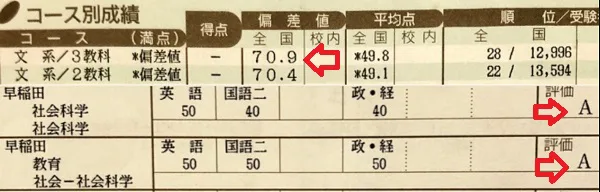
現役の時に偏差値40ほど、日東駒専に全落ちした私。
しかし浪人して1ヶ月で「英語長文」を徹底的に攻略して、英語の偏差値が70を越え、早稲田大学に合格できました!
私の英語長文の読み方をぜひ「マネ」してみてください!
・1ヶ月で一気に英語の偏差値を伸ばしてみたい
・英語長文をスラスラ読めるようになりたい
・無料で勉強法を教わりたい
こんな思いがある人は、下のラインアカウントを追加してください!
筆者は現役時代、偏差値40ほどで日東駒専を含む12回の受験、全てに不合格。
原因は「英語長文が全く読めなかったこと」で、英語の大部分を失点してしまったから。
浪人をして英語長文の読み方を研究すると、1ヶ月で偏差値は70を超え、最終的に早稲田大学に合格。
「1ヶ月で英語長文がスラスラ読める方法」を指導中。
⇒【秘密のワザ】1ヵ月で英語の偏差値が40から70に伸びた方法はこちら
⇒【1カ月で】早慶・国公立の英語長文がスラスラ読める勉強法はこちら
⇒【速読】英語長文を読むスピードを速く、試験時間を5分余らせる方法はこちら











